
From the fan on your ceiling, the wheels on your bike, to the planet Earth you’re residing on. Many things around you are going round and round. Often times, when initiated into the field of classical mechanics, we focus so much on motion that moves you from point A to point B, that we lose sight of the type of motion that whirls. Rotational mechanics is a very important topic in Physics where we study the spinning of objects, which not only answers our curious questions regarding daily life phenomena, but also used in the design of important machines such as cars and planes.
Prerequesites:
To have a better understanding of the material presented in this post, it is recommended that you have some understanding of the following topics in Mathematics and Physics:
- Basic Kinematics and Dynamics
- Basic Calculus
- Basic Vectors
The Perfect Analogy 🌼
As with any analysis of natural phenomena, it is useful to figure out useful definitions for quantities relevant to the discussion of it. In the case of rotational motion, you will find many analogous quantities to those of translational motion as they both describe physical motion. Even the equations that govern them can be astonishingly similar, keeping this fact in mind can really help you get used to the subject and achieve excellence in it.
Kinematics 👟
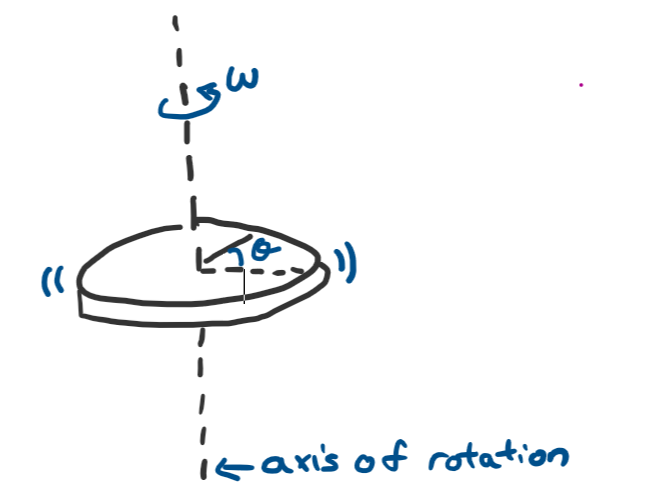
Whenever an object is spinning, we usually denote an axis of rotation which is the “imaginary line” that the objects spins around. Whilst distance is a measure of how far we move, the angle of rotation \(\theta\) measures how far we turn.
Similarly, angular velocity \(\omega\) which obviously parallels velocity tells us how fast something is turning while angular acceleration \(\alpha\) tells us how fast something is increasing in angular velocity. This can be expressed mathematically using derivatives where \(\omega = \frac{d\theta}{dt}\) and \(\alpha = \frac{d\omega}{dt} = \frac{d^2\theta}{dt^2}\).
Kinematic Equations 🏃🏽
Seeing how \(\theta\),\(\omega\) and \(\alpha\) are related in the same ways the displacement \(x\), velocity \(v\) and acceleration \(a\) are related, the equations derived from this relation are the same as well.
\[\omega = \omega_0 + \alpha t\] \[\theta = \theta_0 + \omega_0 t + \frac{1}{2} \alpha t^2\]When the angular acceleration is constant, the “suvat” equations in translational kinematics hold true for its rotational counterpart.
Angular Momentum 📐
Now let’s try something interesting, get yourself two 1 litre bottles filled with water and find an office chair that you can spin yourself with. Now extend your hands outwards while on the office chair whilst holding in each hand a water bottle. Use your legs to provide yourself some spin and lift them off the ground. Finally pull both your arms towards your chest and observe how much faster you can spin. (Make sure you do this in some open space without any fragile objects). Want to know why pulling in your arms made you spin faster? Let’s learn about angular momentum.
Angular momentum is the degree to which some spinning object wants to keep spinning or how hard it is to stop it from spinning. For a single particle, the angular momentum can be quantified by the product between the distance the rotating object is from the axis of rotation \(\vec{r}\) and its translational momentum \(\vec{p}\).
\[\vec{L} = \vec{r}\times \vec{p} = m \vec{r} \times \vec{v}\]A useful fact about angular momentum is that in a closed system, this quantity remains constant. This means that if u have a bunch of objects rotating, and nothing outside of these bunch of objects interferes with them, the sum of their “insistence of spinning” will remain the same.
This is why you spin faster when you pull your heavy water bottles inwards, since \(r\), decreases, and \(L\) is constant, the magnitude of \(v\) must increase, causing you to spin faster.
(Side note) If you are familiar with cross products, notice that the angular momentum vector is perpendicular to both the position vector \(\vec{r}\) and the velocity vector \(\vec{v}\), pointing out of the plane of the orbit. You can use the right hand rule to determine whether it points out of the plane or inwards. The visualization of the angular momentum vector will immensely help the understanding of further topics involving rotational mechanics.
Dynamics ⚽
Center of Mass ⚖️
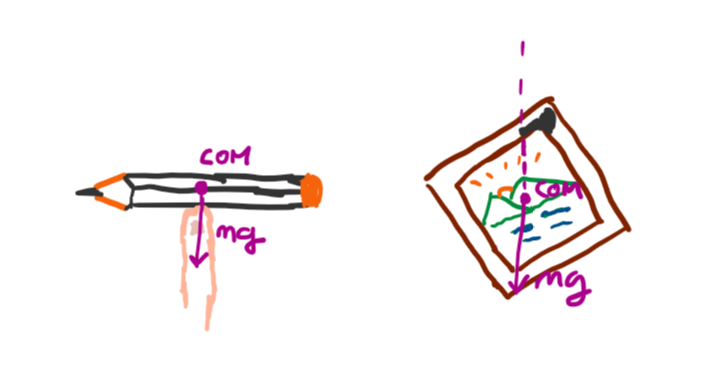
Ever tried balancing a pencil on the tip of your finger? You will find that there is a point where your finger has to be above, no matter the orientation of your pencil, for the pencil to balance. Same goes for hanging an object on a pin to a wall, the pin will always be directly above a point called the center of gravity or the center of mass. The center of mass is essentially a point where you can treat the object’s mass to be concentrated at. It is also the point where you can assume the object’s gravity acts upon said object.
The center of mass is found by summing up the product of the masses and the distances the masses are from a designated point (self-chosen origin) and dividing that product by the total mass of the system. This can be illustrated by the following expression:
\[\vec{R}_{CM}= \frac{ \sum^N_i m_i \vec{r}_i }{ \sum^N_{i} \vec{r}_i }\]Don’t be intimidated by the equation above, intuitively you can rationalize that the more mass is closer to a certain location within the system, the closer the center of mass is to that location.
Moment of Inertia ⏳
Interestingly, you can understand mass as how hard it is to make an object to move faster. The doppleganger of mass in rotational mechanics is something we call the Moment of Inertia \(I\). The greater the moment of inertia, the harder it is to make something spin faster in a specific direction.
\[I = \sum^N_\alpha m_\alpha\rho^2_\alpha\]From this equation you can actually see that the further the mass is distributed from the axis of rotation, the greater the moment of inertia is. So if the heavy parts of a system is far away from the axis of intended rotation, it becomes incredibly hard to turn.
A single object can have multiple different values for its moment of inertia, can you guess why? Because we need to specify the axis of rotation. Its easier to spin about the axis of rotation where the mass is distributed close to it compared to a different axis where the mass is further away from it. This largely governs how an object spins.
Using this notation, we can also give another relation that describes the angular momentum that parallels the translational equation \(\vec{p} = m\vec{v}\).
\[L = I \vec{\omega}\]Moments 🖼️
Have you ever noticed that when you try to open a door by pushing it near the hinge, it is way harder to open compared to when you push the door far away from the hinge. This can be explained by understanding the concept of moments. The moment is the turning effect of the force. The moment caused by a force can be calculated by taking the cross product of the perpendicular distance from a point to the line of action of the force (sometimes called the lever arm) with the force vector.
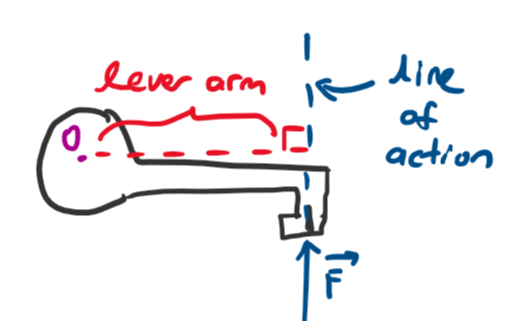
Torque is the moment of a force denoted by \(\tau\) (tau). It is also the rotational equivalent for force as it also follows the relation
\[\vec{\tau} = I \vec{\alpha}\]Torque allows the spinning of an object to speed up or slow down.
Work and Energy ⚡
Energy is defined as the ability to do work. And it is obvious from turbines to motors in generators that things that stay put in one place and spin are capable of doing tons of work. Therefore there should be rotational kinetic energy that the translational kinetic energy formula does not take into account. That formula is the following.
\[E = \frac{1}{2} I\omega^2\]therefore the total kinetic energy of a moving object is the sum of its translational and rotational kinetic energy.
Conclusion ✨
It is pretty hard to cram all of the concepts in this vast field in physics into one blog post and do it justice. What I have presented is prelude to the many interesting theorems that are ever present throughout the subject. I have included links in the following section if you intend to learn more about rotational mechanics. I hope that through this post you have been illuminated by the wondrous science of spinning objects.